start_time <- Sys.time()
library(tidyverse)
library(here)
library(fixest)
library(kableExtra)
library(microbenchmark)
data <-
read_rds(here("..", "output",
"data_reports.rds")) %>%
filter(year %in% 2016:2023) %>%
mutate(week = week(date))Discussion on estimation
In this script, I do some computation to support a discussion on estimation in the appendix.
Clearly not very important
Describe the count data briefly
Compute the frequency of 0 and 1 etc
frequency <- data %>%
filter(covid_phase == "Pre-pandemic") %>%
count(reports_dv) %>%
mutate(freq = n / sum(n))
frequency %>% kbl()| reports_dv | n | freq |
|---|---|---|
| 0 | 3577006 | 0.9778386 |
| 1 | 78061 | 0.0213394 |
| 2 | 2875 | 0.0007859 |
| 3 | 123 | 0.0000336 |
| 4 | 8 | 0.0000022 |
| 5 | 1 | 0.0000003 |
Export to latex, I just copy paste it
frequency %>% kbl(format = "latex", booktabs = TRUE, longtable = TRUE, align = "lcc") %>%
kable_styling(latex_options = c("hold_position"))Discussion
My dependent variable – crime counts per day per neighborhood – shows a high prevalence of zeros (98%) and ones (2%), with only a few observations of higher counts.
Given this high prevalence of zeros and a discrete count distribution, estimating the effect of temperature on DV crime requires careful consideration of the appropriate econometric model. Some models are more suitable than others, I estimate and discuss the following, and compare the estimates of the following model:
reports_dv ~ tmean | prec_quintile + rh_quintile + wsp_quintile + ageb + year^month + day_of_week + day_of_year
OLS-Based Transformations (Linear Regression Approaches))
- OLS with Raw Count: Direct application of OLS to count data without any transformation, treating counts as continuous outcomes.
- OLS with Quartic Root Transformation: Applies a quartic root to count data to reduce skewness and stabilize variance before using OLS.
- Interpretation becomes more complex but generally speaks to the proportional change in the quartic root of crime counts.
- The quartic-root serves as a proxy for a logarithmic transformation for positive numbers, avoiding either dropping zeroes or adding an arbitrary small amount. It is a common transformation for variables with outliers that could disproportionately influence the estimates, such as crime rates, saving rates, or earnings (Ashraf et al. 2015; Velasquez 2019).
- OLS with Arcsinh Transformation: Utilizes the inverse hyperbolic sine transformation for count or skewed data, capable of handling zeros and negative values, before applying OLS.
- The inverse hyperbolic sine transformation is another way to deal with zeros and negative values while stabilizing variance.
- Similar to the log transformation, for large values, but smoother for values around zero.
- OLS with Log(y+1) Transformation: Applies a log transformation (log(y+1)) to handle zero counts and reduce skewness, making the distribution more suitable for OLS analysis.
- Coefficients can be interpreted as approximate percentage changes in crime counts for a one-unit change in temperature, valid for small coefficient values.
Binary Response Models
- Linear Probability Model (LPM): Uses OLS directly on a binary outcome, providing probability estimates for the occurrence of an event. Does not handle the excess zeros well.
- Logit (Logistic Regression): Non-linear model estimating the probability of a binary outcome, such as the occurrence of an event (1) or not (0).
Count Data Models
- Poisson Count Model: Designed explicitly for count data presumed to follow a Poisson distribution, making it a natural choice. However, assumes that the count’s variance equals its mean (equidispersion).
- Poisson Pseudo-Maximum Likelihood (PPML): A robust alternative to Poisson that can be used even when the equidispersion assumption does not hold, and it handles zeros naturally.
- Negative Binomial Regression (NegBin): Handles overdispersion in count data by introducing an additional parameter.
Models for Count Outcomes with Excess Zeros
- Zero-Inflated Models: Combines a count model (like Poisson or NegBin) with a binary model to handle excess zeros by modeling the occurrence of zeros separately. Useful when the data show more zeros than expected, which is not the case here.
- Hurdle Models: Similar to Zero-Inflated models but explicitly models the decision process as two stages: whether an event occurs and the count of events given that it occurs.
PPML
In our context, the Poisson Pseudo-Maximum Likelihood (PPML) estimation method is often preferred over the simple Poisson regression model for different reasons:
Handling Over-dispersion: The simple Poisson model assumes that the mean and variance of the dependent variable are equal. Over-dispersion occurs when the variance exceeds the mean, leading to inefficiency and biased standard errors in the simple Poisson model. PPML can handle over-dispersion more effectively, providing more reliable estimates. The “pseudo” aspect of PPML comes from the use of a quasi-likelihood approach, which doesn’t require strict distributional assumptions like the simple Poisson model.
Heteroskedasticity: PPML is robust to heteroskedasticity. Unlike the simple Poisson model, which assumes constant variance across observations, PPML can produce consistent estimates even when this assumption is violated.
So, while the simple Poisson model is useful for count data that strictly follows the Poisson distribution, PPML offers a more flexible and robust alternative.
Negbin
In addition, when dealing with zero-inflated data, additional models like a Negative Binomial might be considered. The Negative Binomial model relaxes the equidispersion assumption of the Poisson model by introducing an extra parameter to account for overdispersion. The estimated θ value of 2 indicates the presence of a moderate level of overdispersion in the count data (the closer to 0, the higher the overdispersion). Specifically, the variance (\(\sigma^2\)) of the count data can be expressed as a function of the mean (\(\mu\)) and the theta parameter (\(\theta\)), with the formula \(\sigma^2 = \mu + \frac{\mu^2}{\theta}\). Plugging \(\theta=2\) into this formula shows that the variance is equal to the mean plus half of the squared mean. This relationship quantifies the extent to which variance exceeds the mean due to overdispersion. The Negative Binomial model is more complex and computationally intensive than the Poisson model.
Comparing Negbin and PPML
I run both a poisson and a negbin, produce a table with over dispersion paramter.
"fepois" <-
fepois(reports_dv ~ tmean |
ageb + year^month + day_of_week + day_of_year,
cluster = ~ ageb,
data = data %>% filter(covid_phase == "Pre-pandemic"))
"fenegbin" =
fenegbin(reports_dv ~ tmean |
ageb + year^month + day_of_week + day_of_year,
cluster = ~ ageb,
data = data %>% filter(covid_phase == "Pre-pandemic"))
# export the table
setFixest_etable(reset = T)
setFixest_dict(
c(reports_dv = "Reports",
tmean = "Temperature",
ageb = "AGEB (Neighborhood)",
month = "Month",
day_of_week = "Day of Week",
day_of_year = "Day of Year",
year = "Year")
)
etable(fepois, fenegbin,
fitstat = ~ my + n + ll + theta) fepois fenegbin
Dependent Var.: Reports Reports
Temperature 0.0335*** (0.0027) 0.0335*** (0.0027)
Fixed-Effects: ------------------ ------------------
AGEB (Neighborhood) Yes Yes
Year-Month Yes Yes
Day of Week Yes Yes
Day of Year Yes Yes
___________________ __________________ __________________
Family Poisson Neg. Bin.
S.E.: Clustered by: AGEB (Neighb.. by: AGEB (Neighb..
Dep. Var. mean 0.02323 0.02323
Observations 3,624,883 3,624,883
Log-Likelihood -380,683.9 -379,979.0
Over-dispersion -- 0.89797
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Export to latex file. The table goes in the appendix.
etable(fepois, fenegbin,
fitstat = ~ my + n + ll + theta,
file = here("..", "output", "tables", "reg_overdispersion.tex"), replace = T,
view = T,
style.tex = style.tex("aer",
model.format = "(i)",
tpt = TRUE,
notes.tpt.intro = "\\footnotesize",
fixef.suffix = " FEs")
)There is only moderate overdispersion in the data, so PPML is the winner. This is confirmed by the negbin who shows basically the same estimate, but with a theta of 1, which is okkk. Despite the technical differences, the interpretation of coefficients in both models is similar, as they both are log-linear models (this means that coefficients can be interpreted in terms of percentage changes).
I now move on, this is an endless topic, and after weeks of tweaking and toying around, I am pretty confident PPML is a good decision.
Negbin takes much much longer, is not common in the lit, and doesnt add much.
Compare evaluation speed of OLS, negbin, and fepois
On my machine, just for info:
- ols 3sec
- fepois 10sec
- fenegbin 30sec
- ppmlhdfe in stata 40sec although in runs multicore
This is all without quintiles etc, takes much longer for the full model.
mbm <- microbenchmark(
"ols" =
{feols(reports_dv ~ tmean |
ageb + year^month + day_of_week + day_of_year,
cluster = ~ ageb,
data = data %>% filter(covid_phase == "Pre-pandemic"))
},
"poisson" =
{fepois(reports_dv ~ tmean |
ageb + year^month + day_of_week + day_of_year,
cluster = ~ ageb,
data = data %>% filter(covid_phase == "Pre-pandemic"))
},
"negbin" =
{fenegbin(reports_dv ~ tmean |
ageb + year^month + day_of_week + day_of_year,
cluster = ~ ageb,
data = data %>% filter(covid_phase == "Pre-pandemic"))
},
times = 5)
mbm %>% summary() %>% kable()| expr | min | lq | mean | median | uq | max | neval |
|---|---|---|---|---|---|---|---|
| ols | 2.489113 | 2.544517 | 2.593344 | 2.563355 | 2.634387 | 2.735346 | 5 |
| poisson | 8.765384 | 8.792592 | 8.871866 | 8.873565 | 8.943986 | 8.983802 | 5 |
| negbin | 28.235519 | 28.453327 | 28.708665 | 28.774231 | 29.018544 | 29.061705 | 5 |
autoplot(mbm)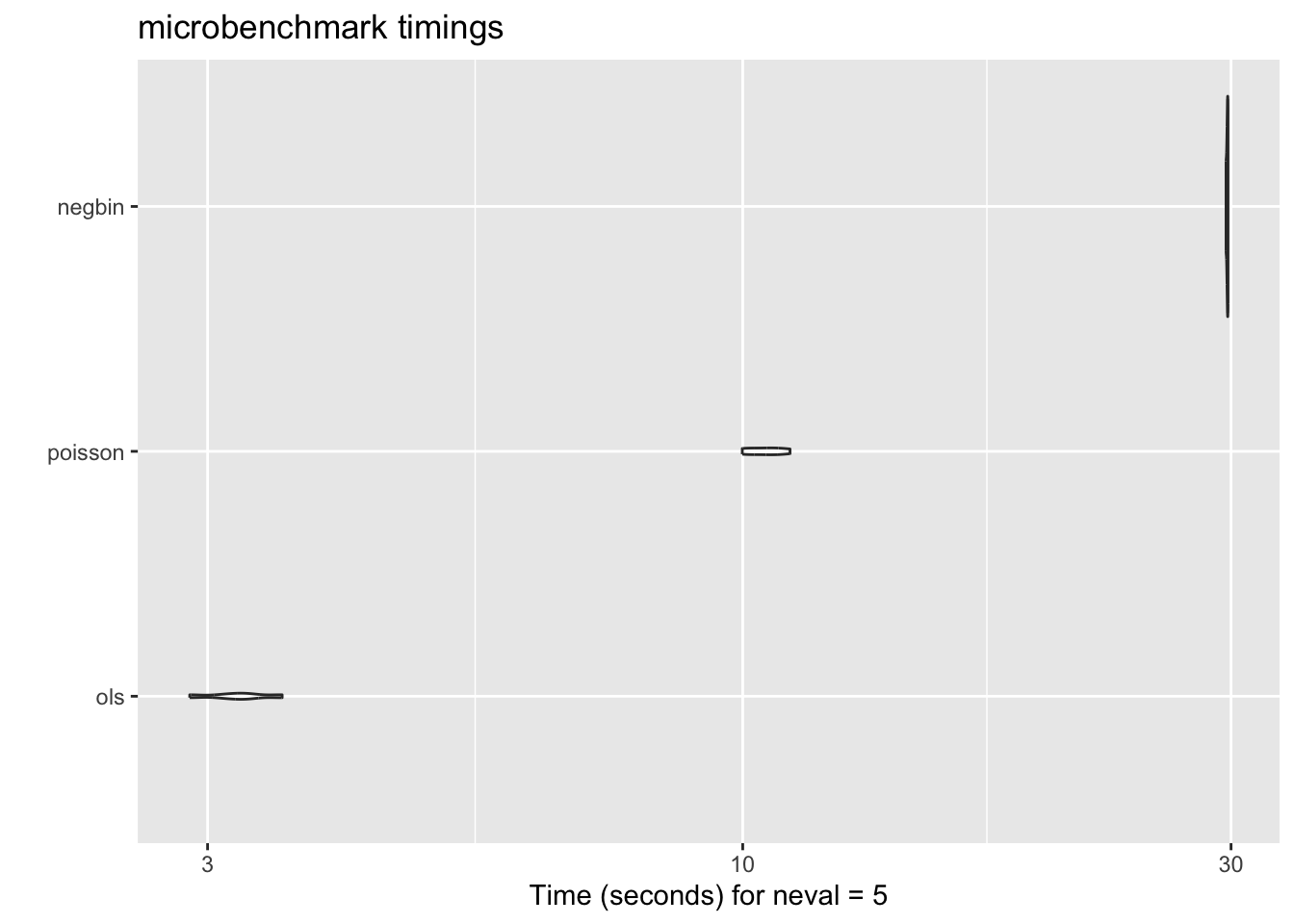
Export data to STATA to compare reg commands
I export my data to stata to compare the results of the R command fixest::fepois with the STATA command ppmlhdfe for the PPML estimation.
data %>%
filter(covid_phase == "Pre-pandemic") %>%
mutate(year_by_month = paste(year, month)) %>%
select(ageb, date, reports_dv, tmean,
year_by_month, year, month, day_of_week, day_of_year) %>%
haven::write_dta(here("..", "output", "data_for_stata.dta"))Using:
ppmlhdfe reports_dv tmean, absorb(ageb year_by_month day_of_week day_of_year) cluster(ageb)in STATA, I get exactly the same results as with fixest::fepois in R.